Magnetic hyperthermia

Magnetic hyperthermia is the name given to an experimental cancer treatment. It is based on the fact that magnetic nanoparticles, when subjected to an alternating magnetic field, produce heat. As a consequence, if magnetic nanoparticles are put inside a tumor and the whole patient is placed in an alternating magnetic field of well-chosen amplitude and frequency, the tumor temperature would raise. This could kill the tumor cells by necrosis if the temperature is above 45 °C, or could improve the efficiency of chemotherapy if the temperature is raised around 42 °C. This treatment is tested on humans only in Germany, but research is done in several laboratories around the world to test and develop this technique.

1 Generalities and definition
2 Influence of nanoparticle size on their domain structure
3 Basic mechanisms involved in the magnetization reversal of magnetic single-domain nanoparticles
4 Models to be used for single-domain nanoparticles
5 Basic mechanisms involved in the magnetization of magnetic multi-domain nanoparticles
6 Models to be used for multi-domain nanoparticles
7 Measuring hyperthermia: in vitro experiments
- 7.1 Producing a high frequency magnetic field
- 7.2 Measuring the temperature and artefacts
8 Materials for magnetic hyperthermia
9 Ex vivo experiments
10 In vivo experiments
- 10.1 Animal testing
- 10.2 Clinical trials
11 See also
12 References
13 External links

Generalities and definition

A general feature of many magnetic materials is to display a magnetic hysteresis when it is measured at a positive magnetic field, then negative, then positive again. The area of this hysteresis loop is dissipated in the environment under the form of thermal energy. This is the energy used in magnetic hyperthermia. The power dissipated by a magnetic material subjected to an alternative magnetic field is often called "Specific Absorption Rate" (SAR) in the community of magnetic hyperthermia; it is expressed in W/g of nanoparticles. The SAR of a given material is then simply given by: 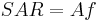$SAR=Af$ , where A is the area of the hysteresis loop and f the frequency of the magnetic field. A is expressed in J/g and is also called "specific losses" of the material. It should be noted that this expression is always true, whatever can be the complexity of determining A. Indeed, as will be more detailed below, A depends on a very complex manner on all the properties of the magnetic material. In the case of magnetic nanoparticles, it depends on their magnetocrystalline anisotropy K, their volume V, the temperature T, the frequency of the magnetic field f, its amplitude 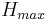$H_{max}$ and on the volumic concentration of the nanoparticles which influences the magnetic interactions between them.^[1]

Influence of nanoparticle size on their domain structure

The size of nanoparticles have a great influence on their magnetic domains. Small sizes nanoparticles are composed of a single domain. Larger ones are composed of several domains minimizing the magnetostatic energy. At intermediate sizes, they display a beautiful magnetic structure called vortex. A rough approximation to determine the size above which a magnetic nanoparticles is not single-domain any more is when its size is above the typical domain wall dimension in the magnetic material, which ranges from a few to a few tens of nanometers. The nature of the domain structure have a profound influence of the hysteresis of the magnetic nanoparticles and, as a consequence of their hyperthermia properties.

Basic mechanisms involved in the magnetization reversal of magnetic single-domain nanoparticles

The goal of this part is to present the basic mechanisms which must be taken into account to describe the reversal of single domain nanoparticles. It is assumed in this part that the nanoparticle display a uniaxial anisotropy.

Reversal by Brownian motion

In hyperthermia application, the nanoparticles are in a fluid, the blood. During in vitro hyperthermia measurements they are generally dispersed in a liquid and form a ferrofluid. They move and rotate randomly in the fluid, a phenomenon called Brownian motion. When a magnetic field is applied to them, magnetic nanoparticles rotate and progressively align with the magnetic field due to the torque generated by the interaction of the magnetic field with the magnetization. This is similar to a compass. The time taken for a magnetic nanoparticle to align with a small external magnetic field is given by the Brown relaxation time: 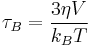$\tau_B = \frac{3 \eta V}{k_BT}$ , where 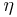$\eta$ is the solvent viscosity. The delay between the magnetic field rotation and the magnetization rotation leads to an hysteresis.

Reversal by thermal activation

The magnetization of the nanoparticle can spontaneously change of orientation under the influence of thermal energy, a phenomenon called superparamagnetism. The magnetization oscillate between its two equilibrium positions. The typical time between two orientation changes is given by the Néel relaxation time 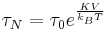$\tau_N = \tau_0 e^{\frac{K V}{k_B T}}$ , where 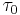$\tau_0$ is an attempt time with a value around 10⁻⁹-10⁻¹⁰ seconds.

Reversal by the suppression of the anisotropy barrier by a magnetic field

The magnetization of the nanoparticle is also reversed when an applied magnetic field is large enough to suppress the energy barrier between the two equilibrium positions, a phenomenon which is known as the Stoner–Wohlfarth model of magnetization reversal.

Combination of the three mechanisms

In the most general case, the reversal of the magnetization is due to a combination of the three mechanisms described above. For instance, let us imagine that a single domain nanoparticle is inside a fluid at room temperature and that a sweeping magnetic field is suddenly applied with a direction opposite to the one of the nanoparticle magnetization. The nanoparticle will at the same time i) rotate in the fluid ii) the barrier between the two equilibrium positions of the magnetization will decrease iii) when the energy barrier becomes of the order of the thermal energy, the magnetization will switch (if the nanoparticle is not already align with the magnetic field due to its physical rotation). There is no simple analytical expression describing this reversal and the properties of the hysteresis loop in this very general case but numerical simulations and analytical expressions can be used in some cases ^[1].

Models to be used for single-domain nanoparticles

The linear response theory

The linear response theory is only valid when the response of the magnetic material is linear with the applied magnetic field and can be thus written under the form 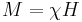$M=\chi H$ , where 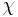$\chi$ is the complex susceptibility of the material. It is thus valid when the applied magnetic field is much smaller than the magnetic field needed to saturate the magnetization of the nanoparticle. It is able to take into account both the reversal by thermal activation and the reversal by Brownian motion.
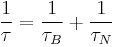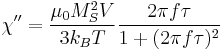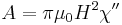The linear response theory uses an average relaxation time $\tau$ , given by $\frac{1}{\tau} = \frac{1}{\tau_B} %2B \frac{1}{\tau_N}$ . The out of phase component of complex susceptibility is then given by $\chi '' = \frac{\mu_0 M_S^2 V}{3 k_B T} \frac{2 \pi f \tau}{1%2B(2 \pi f \tau)^2}$ . The hysteresis loop is then an ellipse with an area given by $A = \pi \mu_0 H^2 \chi ''$ .

The Stoner–Wohlfarth model and the maximum area

The Stoner–Wohlfarth model allows one to calculate the hysteresis loop of magnetic nanoparticles at T=0 with the assumption that the nanoparticles are fixed in the magnetic field (the Brownian motion is neglected) and magnetically independent. Its main interest is to predict the maximum hysteresis area for independent nanoparticles with given properties. Indeed, the addition of thermal energy or Brownian motion only leads to a decrease of the hysteresis loop area (see below).
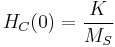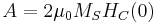The Stoner–Wohlfarth model predicts that the coercive field at T=0 of an assembly of nanoparticles with randomly oriented axes is given by $H_C(0) = \frac{K}{M_S}$ . The area of the hysteresis is approximatively $A = 2\mu_0 M_S H_C(0)$ .

Extension of the Stoner–Wohlfarth model to include temperature and frequency

Extensions of the Stoner–Wohlfarth model have been done to include the influence of the temperature and frequency on the hysteresis loop. These extensions are only valid is the effect of the temperature or of the frequency are small, i.e. if 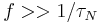$f >> 1/\tau_N$ . Numerical simulations have shown that, in this case, the expression of the coercive field for randomly oriented nanoparticles is^[2]^[3] 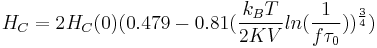$H_C = 2 H_C(0) (0.479-0.81(\frac{k_B T}{2 K V} ln(\frac{1}{f \tau_0}))^{\frac{3}{4}})$ . One can see from this expression that the effect of the temperature is simply to reduce the coercive field of the nanoparticles.

Basic mechanisms involved in the magnetization of magnetic multi-domain nanoparticles

In multi-domain nanoparticles the basic ingredients to describe the magnetization reversal are the nucleation of new domains and the propagation of domain walls. Both mechanisms are strongly influenced by the structural defects at the surface or inside the nanoparticles and make difficult any quantitative prediction of the hysteresis loops shape and area from intrinsic parameters of the magnetic nanoparticles.

Models to be used for multi-domain nanoparticles

At low magnetic field, the hysteresis loop is expected to be a Rayleigh loop. In this case, the hysteresis area is 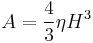$A = \frac{4}{3} \eta H^3$ , where 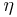$\eta$ is the Rayleigh constant.

Measuring hyperthermia: in vitro experiments

Producing a high frequency magnetic field

Two basic means to produce the high frequency field necessary to study hyperthermia can be used: the coil and the electromagnet. For the "coil" way, a very simple method to get the high frequency magnetic field is to use an induction furnace, which precisely used a high-frequency magnetic field to heat materials. It is however conceived to work at a single frequency and requires a water cooling system. It is also possible to build electromagnets or coils able to work at various frequencies at the condition to use variable capacitors.^[4] It is also possible to get rid of the cooling system in coils at the condition to build them with Litz wire.^[4]

Measuring the temperature and artefacts

A platinum or semi-conductor resistance thermometer in a high-frequency magnetic field is self-heated and leads to erroneous temperature measurements. Temperature measurements in hyperthermia can be made using alcohol thermometer or optic fiber thermometers.
A colloidal solution heated by an external magnetic field will be subject to convection phenomena so the temperature inside the calorimeter is not homogeneous. Shaking of the colloidal solutions at the end of a measurement or average on several temperature probes can ensure a more accurate temperature measurement.

Materials for magnetic hyperthermia

Thermoseeds

Iron oxide nanoparticles

The most widely used magnetic nanoparticles for hyperthermia consists in iron oxide nanoparticles. Similar nanoparticles are used as MRI contrast agent. They are in the context of MRI called "Superparamagnetic Iron Oxide Nanoparticles", or SPION. The main interest of these nanoparticles are their biocompatibility and their stability with respect to oxidation. The nanoparticles displaying the largest hysteresis area so far are the SPIONs synthesized by magnetotactic bacteria,^[5] with A = 2.3 mJ/g although chemically synthesized nanoparticles reach values up to A = 1.5 mJ/g^[6]

Metallic nanoparticles

The higher magnetization of metallic nanoparticles of Co, Fe or FeCo compared to iron oxide increases the maximum SAR values which can be reached using them in hyperthermia applications. A = 1.5 mJ/g has been reported for FeCo nanoparticles,^[3] A = 3.25 mJ/g for Co nanoparticles^[7] and A=5.6 mJ/g for Fe nanoparticles.^[8] The main issue with respect to metallic nanoparticles concerns their protection against oxidation and their eventual toxicity.

Ex vivo experiments

Ex vivo experiments in hyperthermia require to make tumor cells absorb magnetic nanoparticles, to place them into an alternative magnetic field and to test their survival rate compared to tumor cells which would follow the same protocol but would not absorb magnetic nanoparticles.

In vivo experiments

Animal testing

Clinical trials

The only hyperthermia setup suitable to treat humans has been developed at the Charité Medical School, Clinic of Radiation Therapy in Berlin.^[9] Andreas Jordan's team in this hospital has performed clinical trials on patients with prostate cancers.^[10]

References

^ ^a ^b J. Carrey, B. Mehdaoui, M. Respaud, J. Appl. Phys. 109, 083921 (2011).
^ J. Garcia-Otero, A. J. Garcia-Bastida, and J. Rivas, J. Magn. Magn. Mater.189, 377 (1998).
^ ^a ^b L.-M. Lacroix, R. Bel Malaki,J. Carrey, S. Lachaize, M. Respaud, G. F. Goya and B. Chaudret, J. Appl. Phys. 105, 023911 (2009), http://arxiv.org/abs/0810.4109
^ ^a ^b L.-M. Lacroix, J. Carrey and M. Respaud, Rev. Sci. Instr. 79, 093909 (2008). http://arxiv.org/abs/0806.3005
^ R. Hergt, R. Hiergeist, M. Zeisberger, D. Schüler, U. Heyen, I. Hilger and W. A. Kaiser, J. Magn. Magn. Mater. 293, 80 (2005).
^ R. Hergt, R. Hiergeist, I. Hilger, W. A. Kaiser, Y. Lapatnikov, S. Margel and U. Richter, J. Magn. Magn. Mater. 270, 345 (2004).
^ M. Zeisberger, S. Dutz, R. Müller, R. Hergt, N. Matoussevitch, and H.Bönneman, J. Magn. Magn. Mater. 311, 224 (2005)
^ B. Mehdaoui, A. Meffre, L.-M. Lacroix, J. Carrey, S. Lachaize, M. Respaud, M. Gougeon, B. Chaudret, http://arxiv.org/abs/0907.4063
^ A. Jordan et al., J. Magn. Magn. Mater. 225, 118 (2001). http://vpd.ms.northwestern.edu/Publications_files/Lei/JMMM_225_118_2001.pdf
^ M. Johannsen et al., Int. J. of Hyperthermia 21, 637 (2005). http://www.anamacap.fr/telechargement/hyperthermie-vo.pdf

External links

Hyperthermia - Cancer therapy hots up article on physics.org